Blog

Find the shortest path in a grid in XNA

Feb 22, 2010  ·  gamedev

I’m playing around with a board game engine in XNA, where players can play missions on a tile-based board. I’m now working on using the A* algorithm to find paths between tiles.

About the game

In the game, players have a number of steps to move in each round, and should be able to select which tile they want to move to.

The game should suggest the shortest possible path to that tile, and mark tiles that are too far away in red, to indicate that they are unavailable.

The pathfinding algorithm is also used by the engine itself, to move enemies on the board. Enemies are controlled by the engine, which can decide where to move, who to attack, etc.

To improve the illusion of intelligence, the algorithm should also be able to select a random path, if multiple options exist. This will give the enemies a random, unpredictable behavior.

Before we continue with how this is implemented, let’s recap.

Board movement

The players and computer controlled enemies can move sideways, but not diagonally:

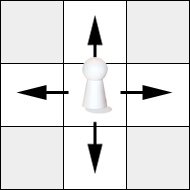
Factors that limit if a game piece can move from one tile to another (tile A to tile B) are:

• B doesn’t exist (the piece would move outside of the board).
• B exists but is marked as None or Nonwalkable (see below).
• B belongs to another room and is separated from A by a wall.
• B is occupied by a piece or furniture (characters can’t stop here).
• B is occupied by a player or enemy (characters can’t pass each other).

All these rules are handled by a bunch of tile-related functions, that take a player or enemy and decide whether or not the character can move to a tile.

Path finding overview

Consider the following map, where a player on the green tile wants to move to the red one:

Since multiple shortest paths exist, I find a random path each time with the following steps:

• Begin at the start tile and set its path length to zero.
• Recursively handle each sibling, as below:
  • If a sibling hasn’t been handled yet, set its path length to the current length + 1.
  • If a sibling has been handled, override its path length if the new length is shorter.
• When no tile can be improved, do the same operations for the end tile back to the start.

I call these two processes spreading (tiles spread the path length to siblings) and tracing (trace the shortest path found while spreading).

Step 1: Spreading

In my game engine, the path-finding operation is started with this Board function:

//Placeholder for the calculated path (not thread safe :)
int[,] pathLengths;

public List<Tile> FindPath(Tile startTile, Tile endTile)
{
    //Abort if start or end tile is null
    if (startTile == null || endTile == null)
    {
        return new List<Tile>();
    }

    //Abort if the end tile is non-stoppable
    if (!endTile.IsStoppable)
    {
        return new List<Tile>();
    }

    //Initialize the path length array
    pathLengths = new int[Tiles.GetLength(0), Tiles.GetLength(1)];
    for (int y = 0; y < pathLengths.GetLength(1); y++)
    {
        for (int x = 0; x < pathLengths.GetLength(0); x++)
        {
            pathLengths[x, y] = int.MaxValue;
        }
    }
    
    //Begin at the start tile
    pathLengths[startTile.BoardPosition.X, startTile.BoardPosition.Y] = 0;
    FindPath_Spread(startTile);

    //Once done, backtrack from the end tile
    List<Tile> result = FindPath_Trace(endTile);

    //Only return the path if it contains the start tile
    if (result.Contains(startTile)) {
         return result;
    }

    return new List<Tile>();
}

This function corresponds to the first part of the numbered list above. We don’t proceed if any tile is null or if the end tile can not be stopped at.

We then initialize a placeholder array with max length values, then run a spread operation from the start tile. Once the spread operation is done, we trace the path.

The function only returns a path if it contains the start tile. If the trace operation can’t reach the start tile, no path should be returned.

The spread operation is recursive and will handle each tile at least once. It consists of two functions, as can be seen below:

private void FindPath_Spread(Tile tile)
{
    FindPath_Spread(tile, tile.TopSibling);
    FindPath_Spread(tile, tile.LeftSibling);
    FindPath_Spread(tile, tile.RightSibling);
    FindPath_Spread(tile, tile.BottomSibling);
}

private void FindPath_Spread(Tile tile, Tile target)
{
    //Abort if any tile is null
    if (tile == null || target == null) {
        return;
    }

    //Abort if no movement is allowed
    if (!tile.CanMoveTo(target)) {    
        return;
    }

    //Get current path lengths
    int tileLength = FindPath_GetPathLength(tile);
    int targetLength = FindPath_GetPathLength(target);

    //Use length if it improves target
    if (tileLength + 1 < targetLength)
    {
        pathLengths[target.BoardPosition.X, target.BoardPosition.Y] = tileLength + 1;
        FindPath_Spread(target);
    }
}

We initialize the operation at the start tile, which has a path length of zero, then spread out to all available siblings.

A sibling is only handled if its path length would be improved. The operation will thus stop automatically once all tiles are as good as they can be.

Step 2: Tracing

After the spread operation, the recursive trace operation is called. It starts at the end tile and finds the shortest way back to the start tile. If it can’t be reached, no path is returned.

The trace operation consists of a single function:

private List<Tile> FindPath_Trace(Tile tile)
{
    //Find the sibling paths
    int tileLength = FindPath_GetPathLength(tile);
    int topLength = FindPath_GetPathLength(tile.TopSibling);
    int leftLength = FindPath_GetPathLength(tile.LeftSibling);
    int rightLength = FindPath_GetPathLength(tile.RightSibling);
    int bottomLength = FindPath_GetPathLength(tile.BottomSibling);

    //Calculate the lowest path length
    int lowestLength =
        Math.Min(tileLength,
        Math.Min(topLength,
        Math.Min(leftLength,
        Math.Min(rightLength, bottomLength))));

    //Add each possible path
    List<Tile> possiblePaths = new List<Tile>();
    if (topLength == lowestLength){
        possiblePaths.Add(tile.TopSibling);
    }
    if (leftLength == lowestLength){
        possiblePaths.Add(tile.LeftSibling);
    }
    if (rightLength == lowestLength) {
        possiblePaths.Add(tile.RightSibling);
    }
    if (bottomLength == lowestLength) {
        possiblePaths.Add(tile.BottomSibling);
    }

    //Continue through a random possible path
    List<Tile> result = new List<Tile>();
    if (possiblePaths.Count() > 0) {
        result = FindPath_Trace(possiblePaths[RandomHelper.GetInt32(0, possiblePaths.Count())]);
    }

    //Add the tile itself, then return
    result.Add(tile);
    return result;
}

FindPath_GetPathLength is a small function that I added to avoid duplicate code:

private int FindPath_GetPathLength(Tile tile)
{
    if (tile == null){
        return int.MaxValue;
    }
    return pathLengths[tile.BoardPosition.X, tile.BoardPosition.Y];
}

Example

Using the map at the beginning of this post, the engine will first parse the map into a game board, as is described in a previous post.

This is how my game (for now) displays the tiles. For now, the walls and doors are missing:

All tiles are walkable to increase the number of “shortest” paths. However, it’s not possible to walk to a dark tile from a light one, much like city blocks.

The green and red tiles just highlight the start and end tile. In the game, they are light grey.

When I run my game-to-be, I auto-generate a path between this green and red tile. As you can see in these images, the game engine suggests different paths each time:

The path finding operation is fast and can handle large board games. However, it wouldn’t be suitable for more complex games, where the world isn’t tile-based.

Discussions & More

If you found this interesting, please share your thoughts on Bluesky and Mastodon. Make sure to follow to be notified when new content is published.